Monopoly

Uniform pricing

All firms, including competitive firms and monopolies, maximize their profits by setting marginal revenue equal to marginal cost.

Marginal Revenue

A firm's marginal revenue curve depends on its demand curve. We will show that a monopoly's marginal revenue curve lies below its demand curve at any positive quantity because its demand curve is downward sloping.

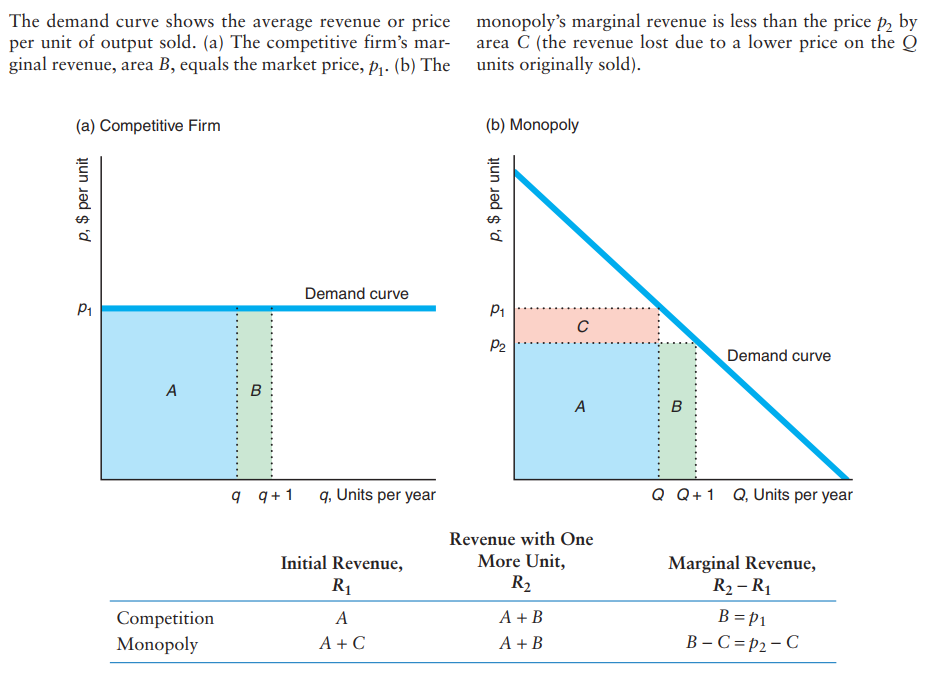
Although the marginal revenue curve is horizontal for a competitive firm, it is downward sloping for a monopoly.

The competitive firm in panel a does not lose an area C from selling an extra unit because its demand curve is horizontal. It is the downward slope of the monopoly's demand curve that causes its marginal revenue to be less than its price.

Deriving Marginal Revenue Curve

For a monopoly to increase its output by \(\Delta Q\), the monopoly lowers its price per unit by \(\frac{\Delta p}{\Delta Q}\) , which is the slope of the demand curve. By lowering its price, the monopoly loses \(\frac{\Delta p}{\Delta Q} * Q\) on the units it originally sold at the higher price (area C), but it earns an additional p on the extra output it now sells (area B). Thus, the monopoly's marginal revenue is

\(MR = p + \frac{\Delta p}{\Delta Q} * Q\).

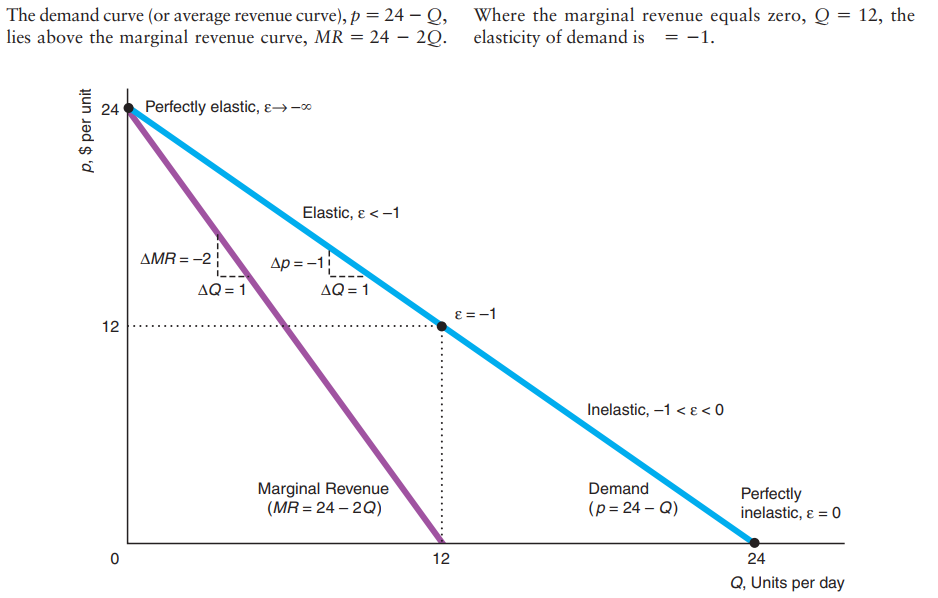
Or we can rewrite this equation in terms of price elasticity of demand,

\(MR = p(1 + \frac{1}{\varepsilon})\).

Any firm maximizes its profit by operating where its marginal revenue equals its marginal cost. Unlike a competitive firm, a monopoly can adjust its price, so it has a choice of setting its price or its quantity to maximize its profit. (A competitive firm sets its quantity to maximize profit because it cannot affect market price.)

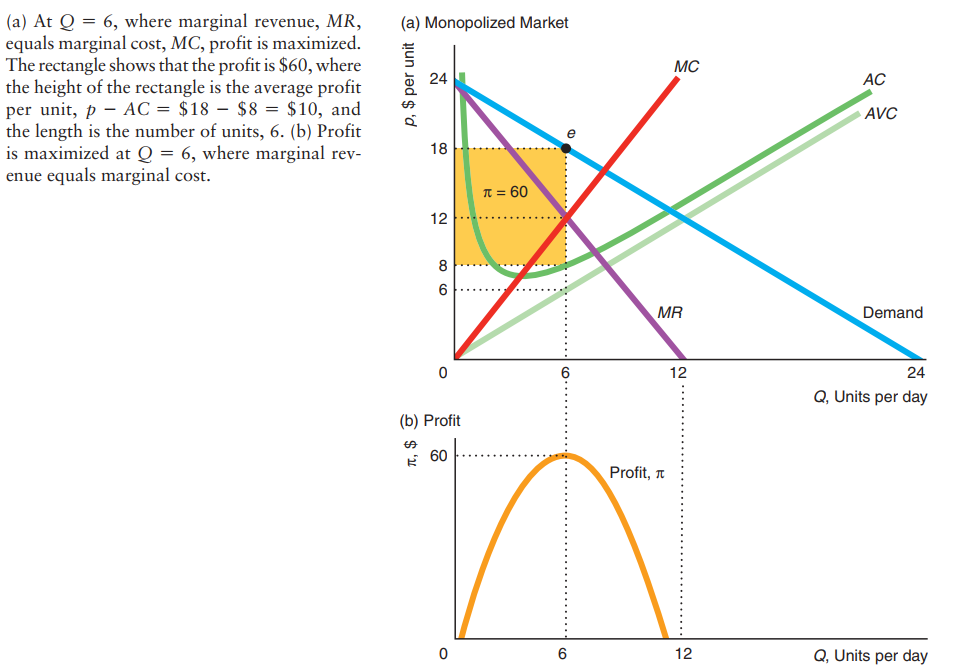
Graphical Approach to maximize profit

All firms, including monopolies, use a two-step analysis to determine the output level that maximizes their profit. First, the firm determines the output, Q, at which it makes the highest possible profit—the output at which its marginal revenue equals its marginal cost. Second, the firm decides whether to produce Q or shut down.

Mathematical Approach

Market power

The degree to which the monopoly raises its price above its marginal cost depends on the shape of the demand curve at the profit-maximizing quantity. If the monopoly faces a highly elastic—nearly flat—demand curve at the profit-maximizing quantity, it loses substantial sales if it raises its price by even a small amount. Conversely, if the demand curve is not very elastic (relatively steep) at that quantity, the monopoly loses fewer sales from raising its price by the same amount.

\(MR = p(1 + \frac{1}{\varepsilon}) = MC\), we can rewrite equation by

Price/Marginal cost ratio: \(\frac{p}{MC} = \frac{1}{1 + \frac{1}{\varepsilon}}\).

Lerner Index: \(\frac{p-MC}{p} = -\frac{1}{\varepsilon}\).

Markup means the more elastic is the demand for the monopolist product, the less monopolist can raise his price above marginal cost. Because if a market demand for the good is very elastic, then big increase in price would drive a lot of consumers to another market. Consumers will substitute the good for another one.

Market Welfare

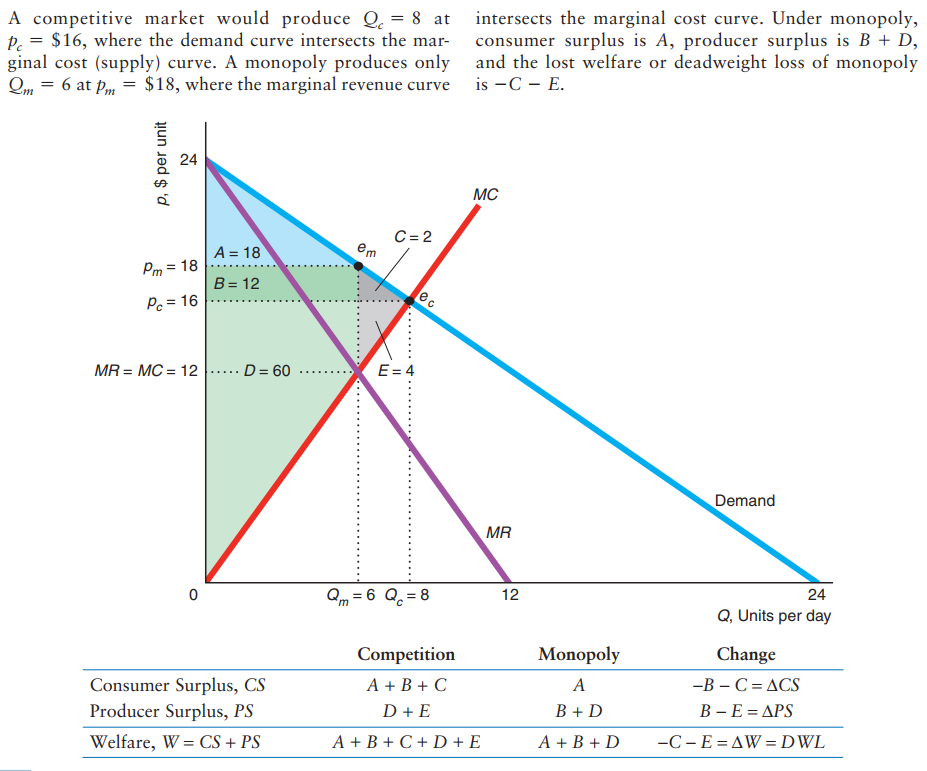
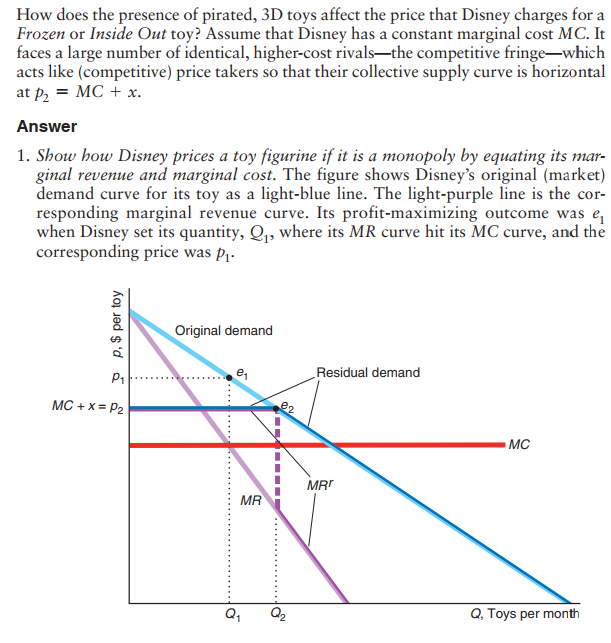
Monopoly example

Natural Monopoly

Monopolies can arise in various ways:

• Cost advantage. A firm can produce efficiently than any other firm at any given quantity produced.
• Government actions: patent. Deadweight loss occurs, when firm get it's patent.

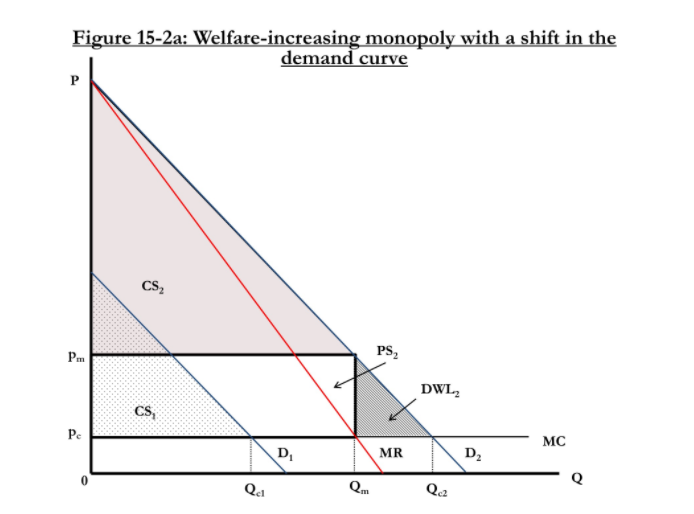
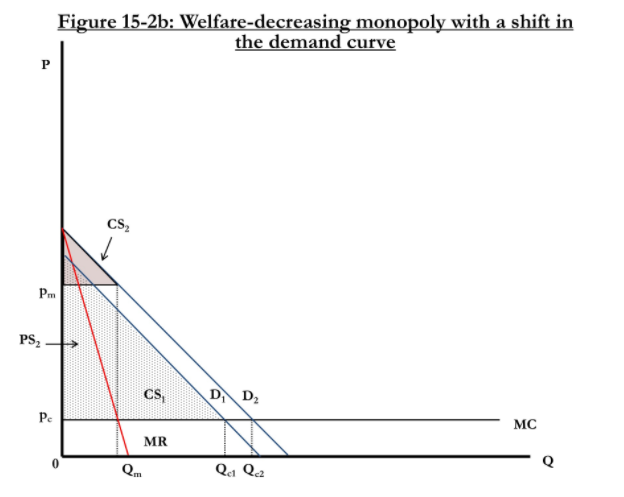
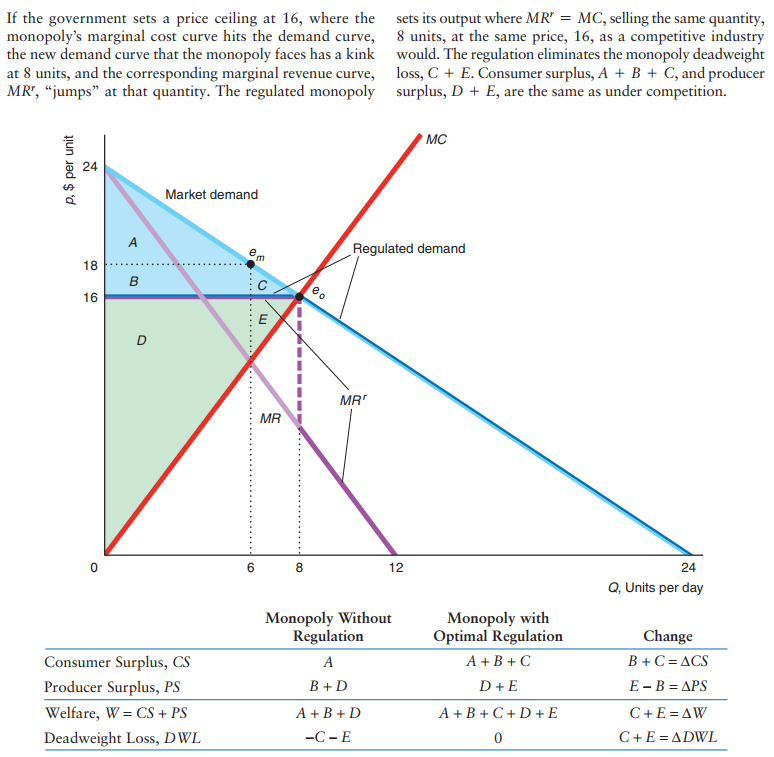
Regulating monopolies